Demo: Spatial data from Slide-seq — Hotspot 0.9.0 documentation

Covered Here¶

Data preprocessing and filtering
Computing Autocorrelation in Hotspot to identify spatial genes
Computing local correlations between spatial genes to identify modules
Plotting modules, correlations, and module scores

[1]:

import numpy as np
import pandas as pd
import hotspot
import matplotlib.pyplot as plt
import matplotlib.colors
import seaborn as sns

# Load the counts and positions
counts_file = 'MappedDGEForR.csv'
pos_file = 'BeadMapping_10-17_1014/BeadLocationsForR.csv'

pos = pd.read_csv(pos_file, index_col=0)
counts = pd.read_csv(counts_file, index_col=0) # Takes a while, ~10min

# Align the indices
counts = counts.loc[:, pos.index]
barcodes = pos.index.values

# Swap position axes
# We swap x'=y and y'=-x to match the slides in the paper
pos = pd.DataFrame(
    {
        'X': pos.ycoord,
        'Y': pos.xcoord*-1,
    }, index=pos.index
)

num_umi = counts.sum(axis=0)

# Filter genes
gene_counts = (counts > 0).sum(axis=1)
valid_genes = gene_counts >= 50
counts = counts.loc[valid_genes]

Creating the Hotspot object¶

To start an analysis, first creat the hotspot object When creating the object, you need to specify:

The gene counts matrix
Which background model to use
The latent space we are using to compute our cell metric
- Here we use the physical barcode positions
The per-cell scaling factor
- Here we use the number of umi per barcode

Once the object is created, the neighborhood graph must be computed with create_knn_graph

The two options that are specificied are n_neighbors which determines the size of the neighborhood, and weighted_graph.

Here we set weighted_graph=False to just use binary, 0-1 weights and n_neighbors=300 to create a local neighborhood size of the nearest 300 barcodes. Larger neighborhood sizes can result in more robust detection of correlations and autocorrelations at a cost of missing more fine-grained, smaller-scale, spatial patterns

[2]:

# Create the Hotspot object and the neighborhood graph

hs = hotspot.Hotspot(counts, model='bernoulli', latent=pos, umi_counts=num_umi)

hs.create_knn_graph(
    weighted_graph=False, n_neighbors=300,
)

Determining genes with spatial variation¶

Now we compute autocorrelations for each gene, using the spatial metric, to determine which genes have the most spatial variation.

[3]:

hs_results = hs.compute_autocorrelations(jobs=16)

hs_results.head()

100%|██████████| 6942/6942 [00:27<00:00, 250.89it/s]

[3]:

	G	EG	stdG	Z	C	Pval	FDR
Gene
Ttr	1.895617e+06	0	4349.885976	435.785413	0.195658	0.0	0.0
Plp1	1.070512e+06	0	4349.885976	246.101150	0.109810	0.0	0.0
Enpp2	9.047060e+05	0	4349.885976	207.983833	0.099028	0.0	0.0
Fth1	9.041625e+05	0	4349.885976	207.858890	0.092616	0.0	0.0
Cartpt	7.867150e+05	0	4349.885976	180.858760	0.084189	0.0	0.0

Grouping genes into spatial modules¶

To get a better idea of what spatial patterns exist, it is helpful to group the genes into modules.

Hotspot does this using the concept of “local correlations” - that is, correlations that are computed between genes between cells in the same neighborhood.

Here we avoid running the calculation for all Genes x Genes pairs and instead only run this on genes that have significant spatial autocorrelation to begin with.

The method compute_local_correlations returns a Genes x Genes matrix of Z-scores for the significance of the correlation between genes. This object is also retained in the hs object and is used in the subsequent steps.

[4]:

# Select the genes with significant spatial autocorrelation
hs_genes = hs_results.index[hs_results.FDR < 0.05]

# Compute pair-wise local correlations between these genes
lcz = hs.compute_local_correlations(hs_genes, jobs=20)

  0%|          | 0/845 [00:00<?, ?it/s]

Computing pair-wise local correlation on 845 features...

100%|██████████| 845/845 [00:05<00:00, 157.16it/s]
100%|██████████| 356590/356590 [59:29<00:00, 99.89it/s]

Now that pair-wise local correlations are calculated, we can group genes into modules.

To do this, a convenience method is included create_modules which performs agglomerative clustering with two caveats:

If the FDR-adjusted p-value of the correlation between two branches exceeds fdr_threshold, then the branches are not merged.
If two branches are two be merged and they are both have at least min_gene_threshold genes, then the branches are not merged. Further genes that would join to the resulting merged module (and are therefore ambiguous) either remain unassigned (if core_only=True) or are assigned to the module with the smaller average correlations between genes, i.e. the least-dense module (if core_only=False)

The output is a Series that maps gene to module number. Unassigned genes are indicated with a module number of -1

This method was used to preserved substructure (nested modules) while still giving the analyst some control. However, since there are a lot of ways to do hierarchical clustering, you can also manually cluster using the gene-distances in hs.local_correlation_z

[5]:

modules = hs.create_modules(
    min_gene_threshold=20, core_only=False, fdr_threshold=0.05
)

modules.value_counts()

[5]:

 4    230
 3    170
-1    143
 2    102
 1    101
 5     63
 6     36
Name: Module, dtype: int64

Plotting module correlations¶

A convenience method is supplied to plot the results of hs.create_modules

[6]:

hs.plot_local_correlations()

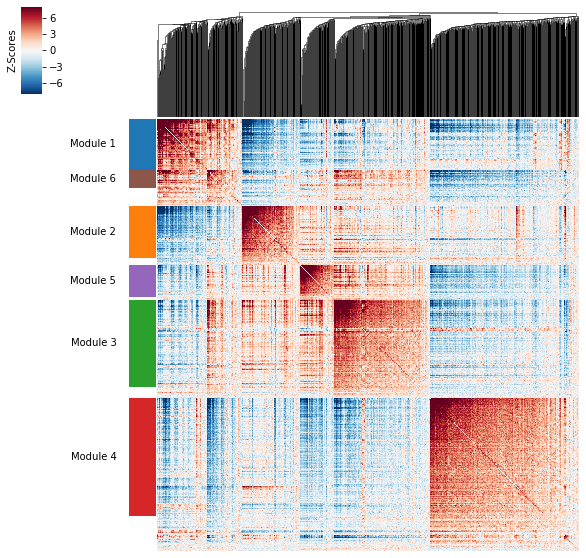
To explore individual genes, we can look at the genes with the top autocorrelation in a given module as these are likely the most informative.

[7]:

# Show the top genes for a module

module = 1

results = hs.results.join(hs.modules)
results = results.loc[results.Module == module]
results.sort_values('Z', ascending=False).head(10)

[7]:

	G	EG	stdG	Z	C	Pval	FDR	Module
Gene
Pcp2	454045.514481	0	4349.885976	104.381015	0.046222	0.0	0.0	1.0
Car8	384470.481798	0	4349.885976	88.386336	0.039361	0.0	0.0	1.0
Itpr1	309992.054843	0	4349.885976	71.264409	0.031606	0.0	0.0	1.0
Pcp4	287016.421190	0	4349.885976	65.982516	0.029496	0.0	0.0	1.0
Pvalb	277574.727119	0	4349.885976	63.811955	0.028504	0.0	0.0	1.0
mt-Cytb	251459.913992	0	4349.885976	57.808392	0.025916	0.0	0.0	1.0
Gpm6b	229566.984067	0	4349.885976	52.775403	0.023639	0.0	0.0	1.0
mt-Nd4	226437.069373	0	4349.885976	52.055863	0.023182	0.0	0.0	1.0
Calb1	198838.797756	0	4349.885976	45.711267	0.020217	0.0	0.0	1.0
Aldoc	187057.748608	0	4349.885976	43.002909	0.019332	0.0	0.0	1.0

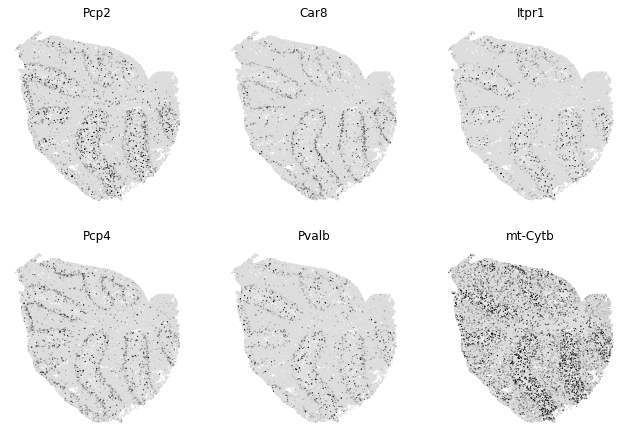
To get an idea of what spatial pattern the module is referencing, we can plot the top module genes’ expression onto the spatial positions

[9]:

# Plot the module scores on top of positions

module = 1

results = hs.results.join(hs.modules)
results = results.loc[results.Module == module]
genes = results.sort_values('Z', ascending=False).head(6).index

fig, axs = plt.subplots(2, 3, figsize=(11, 7.5))

cmap = matplotlib.colors.LinearSegmentedColormap.from_list(
    'grays', ['#DDDDDD', '#000000'])

for ax, gene in zip(axs.ravel(), genes):

    expression = np.log2(hs.counts.loc[gene]/hs.umi_counts*45 + 1) # log-counts per 45 (median UMI/barcode)

    vmin = 0
    vmax = np.percentile(expression, 95)
    vmax = 2

    plt.sca(ax)
    plt.scatter(x=hs.latent.iloc[:, 0],
                y=hs.latent.iloc[:, 1],
                s=2,
                c=expression,
                vmin=vmin,
                vmax=vmax,
                edgecolors='none',
                cmap=cmap
               )

    for sp in ax.spines.values():
        sp.set_visible(False)

    plt.xticks([])
    plt.yticks([])
    plt.title(gene)

Summary Module Scores¶

To aid in the recognition of the general behavior of a module, Hotspot can compute aggregate module scores.

[10]:

module_scores = hs.calculate_module_scores()

module_scores.head()

  0%|          | 0/6 [00:00<?, ?it/s]

Computing scores for 6 modules...

100%|██████████| 6/6 [01:30<00:00, 12.98s/it]

[10]:

	1	2	3	4	5	6
barcodes
CGTACAATTTTTTT	0.822729	-0.443706	-0.094899	-0.414559	-0.198448	0.180391
TTCGTTATTTTTTT	1.232227	-0.421417	-0.254999	-0.472261	-0.213982	0.299108
CAAACCAACCCCCC	0.607751	-0.312146	-0.166309	0.234819	-0.328414	0.367822
TCTTTTCACCCCCC	1.286320	-0.491108	-0.053740	-0.736092	-0.096152	0.377854
GGATTGAACCCCCC	0.133101	-0.544696	-0.157040	-0.326436	-0.133297	0.334153

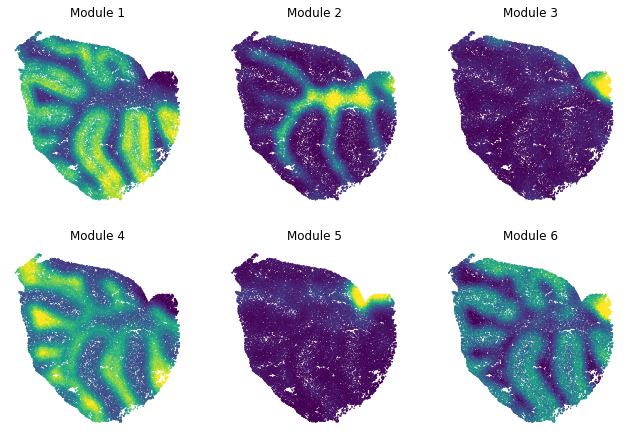
Here we can visualize these module scores by plotting them over the barcode positions:

[11]:

# Plot the module scores on top of positions

fig, axs = plt.subplots(2, 3, figsize=(11, 7.5))

for ax, module in zip(axs.ravel(), range(1, hs.modules.max()+1)):
    scores = hs.module_scores[module]

    vmin = np.percentile(scores, 1)
    vmax = np.percentile(scores, 99)

    plt.sca(ax)
    plt.scatter(x=hs.latent.iloc[:, 0],
                y=hs.latent.iloc[:, 1],
                s=2,
                c=scores,
                vmin=vmin,
                vmax=vmax,
                edgecolors='none'
               )

    for sp in ax.spines.values():
        sp.set_visible(False)

    plt.xticks([])
    plt.yticks([])
    plt.title('Module {}'.format(module))

Demo: Spatial data from Slide-seq¶