Demo: Transcriptional Patterns in CD4 T Cells — Hotspot 0.9.0 documentation

Covered Here¶

Data preprocessing and filtering
Computing Autocorrelation in Hotspot to identify lineage-related genes
Computing local correlations between lineage genes to identify heritable modules
Plotting modules, correlations, and module scores

[1]:

import warnings; warnings.simplefilter('ignore')

import hotspot
import h5py
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.sparse as sparse

from sklearn.decomposition import PCA
from umap import UMAP

/data/yosef2/users/david.detomaso/programs/anaconda3/lib/python3.6/site-packages/sklearn/externals/joblib/__init__.py:15: DeprecationWarning: sklearn.externals.joblib is deprecated in 0.21 and will be removed in 0.23. Please import this functionality directly from joblib, which can be installed with: pip install joblib. If this warning is raised when loading pickled models, you may need to re-serialize those models with scikit-learn 0.21+.
  warnings.warn(msg, category=DeprecationWarning)

Load data from h5 file and extract CD4 T cells¶

[2]:

def load_data():
    f = h5py.File("5k_pbmc_protein_v3_filtered_feature_bc_matrix.h5", 'r')

    barcodes = f['matrix/barcodes'][:].astype('str')

    names = f['matrix/features/name'][:].astype('str')
    ens_ids = f['matrix/features/id'][:].astype('str')
    f_type = f['matrix/features/feature_type'][:].astype('str')
    genome = f['matrix/features/genome'][:].astype('str')
    pattern = f['matrix/features/id'][:].astype('str')
    read = f['matrix/features/read'][:].astype('str')
    sequence = f['matrix/features/sequence'][:].astype('str')

    features = pd.DataFrame({
        'Name': names,
        'Id': ens_ids,
        'Type': f_type,
        'Genome': genome,
        'Pattern': pattern,
        'Read': read,
        'Sequence': sequence,
    })

    data = f['matrix/data'][:]
    indices = f['matrix/indices'][:]
    indptr = f['matrix/indptr'][:]
    shape = f['matrix/shape'][:]


    matrix = sparse.csc_matrix(
        (data, indices, indptr),
        shape=shape
    )

    # Split the matrix into the mRNA and the antibody counts
    mRNA_rows = features.Type == "Gene Expression"
    i_mRNA_rows = mRNA_rows.values.nonzero()[0]
    protein_rows = features.Type == "Antibody Capture"
    i_protein_rows = protein_rows.values.nonzero()[0]

    proteins = matrix[i_protein_rows, :]
    mRNA = matrix[i_mRNA_rows, :]

    del matrix

    features_genes = features.loc[mRNA_rows]
    features_proteins = features.loc[protein_rows]

    del features

    # Gene filtering
    num_umi = mRNA.sum(axis=0)
    num_umi = np.array(num_umi).ravel()

    num_umi_mat = sparse.lil_matrix((len(num_umi), len(num_umi)))
    num_umi_mat.setdiag(1/num_umi)

    mito_genes = [x.lower().startswith('mt-') for x in features_genes.Name.values.astype('str')]
    mito_genes = np.array(mito_genes)

    mito_count = np.array(mRNA[mito_genes].sum(axis=0)).ravel()
    mito_percent = mito_count / num_umi * 100

    proteins_df = pd.DataFrame(
        proteins.toarray(), index=features_proteins.Id.values.astype('str'),
        columns=barcodes.astype('str')
    ).T

    features_genes = features_genes.set_index("Id")[["Name"]].rename({"Name": "GeneSymbol"}, axis=1)

    num_umi = pd.Series(num_umi, index=barcodes)
    mito_percent = pd.Series(mito_percent, index=barcodes)

    return mRNA, features_genes, barcodes, num_umi, mito_percent, proteins_df

mRNA, genes, barcodes, umi_counts, mito_percent, proteins = load_data()

Extract the CD4 T Cells based on surface protein abundance¶

[3]:

def clr(x):

    x = np.log(x+1)
    x = x.subtract(x.mean(axis=1), axis=0)

    return x

proteins_clr = clr(proteins)

is_cd4 = (
    (proteins_clr['CD14'] < 2) &
    (proteins_clr['CD4'] > 3) &
    (proteins_clr['CD3'] > 2.5)
).values

# Further filter by Mito-Percent and Num-Umi
is_healthy = (
    (umi_counts > 3100) &
    (mito_percent < 16)
)

is_cd4 = is_cd4 & is_healthy
is_cd4_ii = is_cd4.values.nonzero()[0]

mRNA_cd4 = mRNA[:, is_cd4_ii]

# Filter genes
gene_counts = np.array((mRNA_cd4 > 0).sum(axis=1)).ravel()
valid_genes = gene_counts > 10

genes = genes.loc[valid_genes]
mRNA_cd4 = mRNA_cd4[valid_genes.nonzero()[0], :]

# Create a counts dataframe and filter other data structures
counts = pd.DataFrame(mRNA_cd4.astype('float64').todense(), columns=barcodes[is_cd4], index=genes.index)
umi_counts = umi_counts.loc[is_cd4]
proteins = proteins.loc[is_cd4]
mito_percent = mito_percent.loc[is_cd4]

print(counts.shape)

(11608, 1486)

Compute a Latent Space with PCA¶

In the Hotspot manuscript, we used scVI for this which has improved performance over PCA. However, to make this notebook easier to run (with less added extra dependencies), we’ll just run PCA using scikit-learn

[4]:

counts_z = counts.divide(umi_counts, axis=1)*umi_counts.median()
counts_z = np.log2(counts_z + 1)
counts_z = counts_z \
    .subtract(counts.mean(axis=1), axis=0) \
    .divide(counts.std(axis=1), axis=0)

model = PCA(n_components=30)
model.fit(counts_z.values.T)

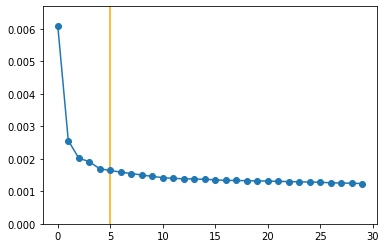
N_COMP = 5

pca_data = model.transform(counts_z.values.T)[:, 0:N_COMP]
pca_data = pd.DataFrame(pca_data, index=counts.columns)

plt.figure()
plt.plot(model.explained_variance_ratio_, 'o-')
plt.vlines([N_COMP], -10, 10, color='orange')
plt.ylim(0, model.explained_variance_ratio_.max()*1.1)

pca_data.head()

[4]:

	0	1	2	3	4
AAACCCAAGGCCTAGA-1	-5.078668	5.228329	-5.669723	-1.739015	4.327831
AAACCCAGTCGTGCCA-1	7.523724	-6.016051	-2.130812	2.785405	2.296527
AAACCCATCGTGCATA-1	6.592712	-5.384366	-2.021500	-3.544320	-4.352100
AAACGAAGTAATGATG-1	12.634856	1.586387	5.746677	8.439582	8.213588
AAACGCTCATGCACTA-1	-5.118548	2.678905	-0.658709	0.258504	1.075994

Creating the Hotspot object¶

To start an analysis, first create the hotspot object When creating the object, you need to specify:

The gene counts matrix
Which background model to use
The latent space we are using to compute our cell metric
- Here we use the reduced, PCA results
The per-cell scaling factor
- Here we use the number of umi per barcode

In this case, only the log-normalized counts are made available. In the Hotspot publication, we used the raw counts and the negative binomial (‘danb’) model. However, to make this example easier to run, here we just supply the log-normalized counts and select the ‘normal’ model.

Once the object is created, the neighborhood is then computed with create_knn_graph

The two options that are specificied are n_neighbors which determines the size of the neighborhood, and weighted_graph.

Here we set weighted_graph=False to just use binary, 0-1 weights (only binary weights are supported when using a lineage tree) and n_neighbors=30 to create a local neighborhood size of the nearest 30 cells. Larger neighborhood sizes can result in more robust detection of correlations and autocorrelations at a cost of missing more fine-grained, smaller-scale patterns.

[5]:

# Create the Hotspot object and the neighborhood graph

hs = hotspot.Hotspot(counts, model='danb', latent=pca_data, umi_counts=umi_counts)

hs.create_knn_graph(
    weighted_graph=False, n_neighbors=30,
)

Determining informative genes¶

Now we compute autocorrelations for each gene, in the pca-space, to determine which genes have the most informative variation.

[6]:

hs_results = hs.compute_autocorrelations(jobs=4)

hs_results.head(15)

100%|██████████| 11608/11608 [00:02<00:00, 5302.93it/s]

[6]:

	C	Z	Pval	FDR
Gene
ENSG00000100450	0.627850	117.356113	0.0	0.0
ENSG00000105374	0.710585	104.588424	0.0	0.0
ENSG00000166710	0.580093	103.624232	0.0	0.0
ENSG00000145425	0.615415	95.902552	0.0	0.0
ENSG00000271503	0.544604	93.774720	0.0	0.0
ENSG00000196154	0.679213	89.212750	0.0	0.0
ENSG00000145649	0.518453	83.451278	0.0	0.0
ENSG00000142676	0.542604	79.965974	0.0	0.0
ENSG00000186468	0.515151	79.432114	0.0	0.0
ENSG00000144713	0.564367	78.765036	0.0	0.0
ENSG00000110700	0.486095	78.423143	0.0	0.0
ENSG00000137441	0.549342	77.677710	0.0	0.0
ENSG00000137154	0.510496	75.949486	0.0	0.0
ENSG00000163682	0.546237	75.687056	0.0	0.0
ENSG00000156482	0.572890	75.220909	0.0	0.0

Grouping genes into lineage-based modules¶

To get a better idea of what expression patterns exist, it is helpful to group the genes into modules.

Hotspot does this using the concept of “local correlations” - that is, correlations that are computed between genes between cells in the same neighborhood.

Here we avoid running the calculation for all Genes x Genes pairs and instead only run this on genes that have significant autocorrelation to begin with.

The method compute_local_correlations returns a Genes x Genes matrix of Z-scores for the significance of the correlation between genes. This object is also retained in the hs object and is used in the subsequent steps.

[8]:

# Select the genes with significant lineage autocorrelation
hs_genes = hs_results.loc[hs_results.FDR < 0.05].sort_values('Z', ascending=False).head(500).index

# Compute pair-wise local correlations between these genes
lcz = hs.compute_local_correlations(hs_genes, jobs=4)

100%|██████████| 500/500 [00:00<00:00, 6036.72it/s]

Computing pair-wise local correlation on 500 features...


100%|██████████| 124750/124750 [00:06<00:00, 19408.02it/s]

Now that pair-wise local correlations are calculated, we can group genes into modules.

To do this, a convenience method is included create_modules which performs agglomerative clustering with two caveats:

If the FDR-adjusted p-value of the correlation between two branches exceeds fdr_threshold, then the branches are not merged.
If two branches are two be merged and they are both have at least min_gene_threshold genes, then the branches are not merged. Further genes that would join to the resulting merged module (and are therefore ambiguous) either remain unassigned (if core_only=True) or are assigned to the module with the smaller average correlations between genes, i.e. the least-dense module (if core_only=False)

The output is a Series that maps gene to module number. Unassigned genes are indicated with a module number of -1

This method was used to preserved substructure (nested modules) while still giving the analyst some control. However, since there are a lot of ways to do hierarchical clustering, you can also manually cluster using the gene-distances in hs.local_correlation_z

[9]:

modules = hs.create_modules(
    min_gene_threshold=15, core_only=True, fdr_threshold=0.05
)

modules.value_counts()

[9]:

-1     102
 1      84
 3      50
 2      46
 7      38
 8      28
 6      28
 11     26
 10     25
 9      21
 5      21
 4      16
 12     15
Name: Module, dtype: int64

Plotting module correlations¶

A convenience method is supplied to plot the results of hs.create_modules

[10]:

hs.plot_local_correlations(vmin=-12, vmax=12)

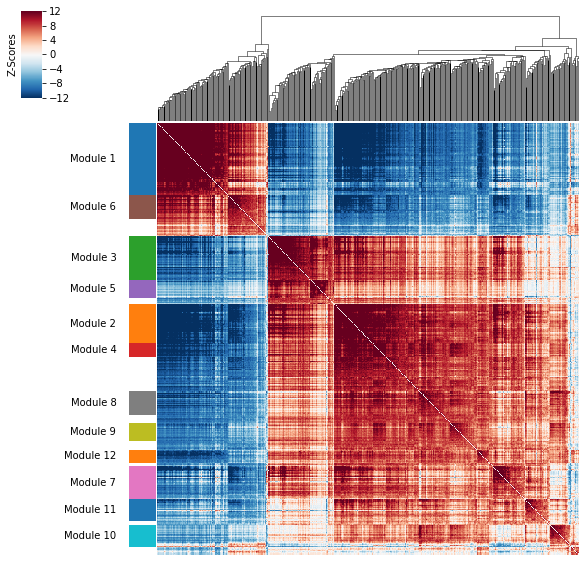
To explore individual genes, we can look at the genes with the top autocorrelation in a given module as these are likely the most informative.

[11]:

# Show the top genes for a module

module = 9

results = hs.results.join(hs.modules)
results = results.loc[results.Module == module]

genes.join(results).sort_values('Z', ascending=False).head(10)

[11]:

	GeneSymbol	C	Z	Pval	FDR	Module
Id
ENSG00000111348	ARHGDIB	0.190166	19.955840	6.668110e-89	3.225142e-87	9.0
ENSG00000172965	MIR4435-2HG	0.213683	18.839304	1.798315e-79	8.091022e-78	9.0
ENSG00000130592	LSP1	0.146799	17.497352	7.504333e-69	3.045815e-67	9.0
ENSG00000163041	H3F3A	0.209711	16.821072	8.551819e-64	3.320051e-62	9.0
ENSG00000175567	UCP2	0.145305	16.110223	1.081210e-58	3.984346e-57	9.0
ENSG00000128340	RAC2	0.109768	16.004655	5.928431e-58	2.164064e-56	9.0
ENSG00000102879	CORO1A	0.126065	15.625450	2.442300e-55	8.723145e-54	9.0
ENSG00000155368	DBI	0.108911	14.900984	1.623814e-50	5.479428e-49	9.0
ENSG00000113387	SUB1	0.127193	14.569997	2.179551e-48	7.187565e-47	9.0
ENSG00000166913	YWHAB	0.095454	13.553244	3.790254e-42	1.154784e-40	9.0

Summary Module Scores¶

To aid in the recognition of the general behavior of a module, Hotspot can compute aggregate module scores.

[12]:

module_scores = hs.calculate_module_scores()

module_scores.head()

  0%|          | 0/12 [00:00<?, ?it/s]

Computing scores for 12 modules...

100%|██████████| 12/12 [00:00<00:00, 28.91it/s]

[12]:

	1	2	3	4	5	6	7	8	9	10	11	12
AAACCCAAGGCCTAGA-1	0.865375	-2.542730	-1.345464	-0.719308	-0.211530	2.787655	-2.001294	-0.901303	-0.016883	-0.010592	-1.065178	-0.573967
AAACCCAGTCGTGCCA-1	-5.822828	5.291330	6.893498	1.929916	0.701222	-2.890965	4.678265	0.784604	1.677809	-0.364284	-0.043380	0.914104
AAACCCATCGTGCATA-1	-2.320981	3.718257	0.163686	1.792634	-0.244096	-2.512566	1.363137	1.236101	1.207091	-0.223936	3.266044	-0.092414
AAACGAAGTAATGATG-1	-8.642907	4.188743	6.984725	1.253119	0.875582	-2.665184	4.113193	1.329732	0.570870	0.624170	-0.132901	2.513368
AAACGCTCATGCACTA-1	2.317936	-2.531565	-1.448488	-1.054099	-0.382518	1.887807	-1.614370	-1.104131	-0.870459	-0.282801	-1.141042	-0.547763

Here we can visualize these module scores by plotting them over a UMAP of the cells

First we’ll compute the UMAP

[13]:

umap_data = UMAP(n_neighbors=30, min_dist=.5).fit_transform(pca_data)
umap_data = pd.DataFrame(umap_data, index=counts.columns, columns=['UMAP1', 'UMAP2'])

plt.figure()
plt.plot(umap_data.UMAP1, umap_data.UMAP2, 'o', ms=2)
plt.xlabel('UMAP-1')
plt.ylabel('UMAP-2')
for sp in plt.gca().spines.values():
    sp.set_visible(False)
plt.xticks([])
plt.yticks([]);

Finally, we plot the module scores on top of the UMAP for comparison

[14]:

fig, axs = plt.subplots(3, 4, figsize=(10, 10))
cax = fig.add_axes(
    [.95, .15, .007, .1]
)

for ax, mod in zip(axs.ravel(), hs.module_scores.columns):
    sc = hs.module_scores[mod]
    # vmin = np.percentile(sc, 5)
    # vmax = np.percentile(sc, 95)
    vmin = -1
    vmax = 1
    plt.sca(ax)
    sc = plt.scatter(
        umap_data.UMAP1, umap_data.UMAP2,
        s=3, c=sc, vmin=vmin, vmax=vmax,
        rasterized=True)
    plt.xticks([])
    plt.yticks([])
    plt.title("Module {}".format(mod))
    for sp in ax.spines.values():
        sp.set_visible(False)

plt.subplots_adjust(hspace=0.4)
plt.colorbar(sc, cax=cax, ticks=[vmin, vmax], label='Module\nScore')
plt.subplots_adjust(left=0.02, right=0.9)

Demo: Transcriptional Patterns in CD4 T Cells¶